AABBTree - Axis-Aligned Bounding Box Trees
AABBTree is a pure Python implementation of a static d-dimensional axis aligned bounding box (AABB) tree. It is inspired by Introductory Guide to AABB Tree Collision Detection from Azure From The Trenches.
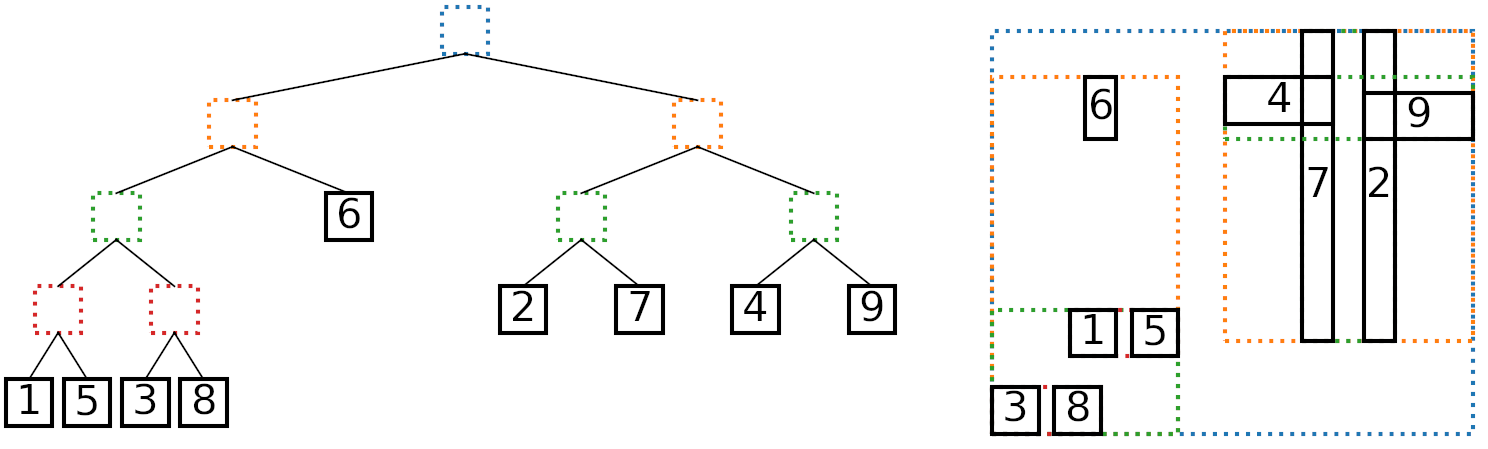
Left: An AABB tree, leaves numbered by insertion order. Right: The AABBs and their bounding boxes.
Installation
AABBTree is available through PyPI and can be installed by running:
pip install aabbtree
To test that the package installed properly, run:
python -c "import aabbtree"
Alternatively, the package can be installed from source by downloading the latest release from the AABBTree repository on GitHub. Extract the source and, from the top-level directory, run:
pip install -e .
The --user flag may be needed, depending on permissions.
Example
The following example shows how to build an AABB tree and test for overlap:
>>> from aabbtree import AABB
>>> from aabbtree import AABBTree
>>> tree = AABBTree()
>>> aabb1 = AABB([(0, 0), (0, 0)])
>>> aabb2 = AABB([(-1, 1), (-1, 1)])
>>> aabb3 = AABB([(4, 5), (2, 3)])
>>> tree.add(aabb1, 'box 1')
>>> tree.does_overlap(aabb2)
True
>>> tree.overlap_values(aabb2)
['box 1']
>>> tree.does_overlap(aabb3)
False
>>> tree.add(aabb3)
>>> print(tree)
AABB: [(0, 5), (0, 3)]
Value: None
Left:
AABB: [(0, 0), (0, 0)]
Value: box 1
Left: None
Right: None
Right:
AABB: [(4, 5), (2, 3)]
Value: None
Left: None
Right: None
API
Class definitions and methods for the AABB and AABBTree.
- class aabbtree.AABB(limits=None)[source]
Bases:
objectAxis-aligned bounding box (AABB)
The AABB is a d-dimensional box.
- Parameters:
limits (iterable, optional) –
The limits of the box. These should be specified in the following manner:
limits = [(xmin, xmax), (ymin, ymax), (zmin, zmax), ...]
The default value is None.
- classmethod merge(aabb1, aabb2)[source]
Merge AABB
Find the AABB of the union of AABBs.
- Parameters:
aabb1 (AABB) – An AABB
aabb2 (AABB) – An AABB
- Returns:
An AABB that contains both of the inputs
- Return type:
AABB
- overlap_volume(aabb)[source]
Determine volume of overlap between AABBs
Let \(\left(l_i^{(1)}, u_i^{(1)}\right)\) be the i-th dimension lower and upper bounds for AABB 1, and let \(\left(l_i^{(2)}, u_i^{(2)}\right)\) be the lower and upper bounds for AABB 2. The volume of overlap is:
\[V = \prod_{i=1}^n \text{max}\left(0, \text{min}\left(u_i^{(1)}, u_i^{(2)}\right) - \text{max}\left(l_i^{(1)}, l_i^{(2)}\right) \right)\]- Parameters:
aabb (AABB) – The AABB to calculate for overlap volume
- Returns:
Volume of overlap
- Return type:
float
- overlaps(aabb, closed=False)[source]
Determine if two AABBs overlap
- Parameters:
aabb (AABB) – The AABB to check for overlap
closed (bool) – Flag for closed overlap between AABBs. For the case where one box is [-1, 0] and the other is [0, 0], the two boxes are interecting if closed is set to True and they are not intersecting if closed is set to False.
- Returns:
Flag set to true if the two AABBs overlap
- Return type:
bool
- property corners
corner points of AABB
- Type:
list
- property perimeter
perimeter of AABB
The perimeter \(p_n\) of an AABB with side lengths \(l_1 \ldots l_n\) is:
\[\begin{split}p_1 &= 0 \\ p_2 &= 2 (l_1 + l_2) \\ p_3 &= 2 (l_1 l_2 + l_2 l_3 + l_1 l_3) \\ p_n &= 2 \sum_{i=1}^n \prod_{j=1\neq i}^n l_j\end{split}\]- Type:
float
- property volume
volume of AABB
The volume \(V_n\) of an AABB with side lengths \(l_1 \ldots l_n\) is:
\[\begin{split}V_1 &= l_1 \\ V_2 &= l_1 l_2 \\ V_3 &= l_1 l_2 l_3 \\ V_n &= \prod_{i=1}^n l_i\end{split}\]- Type:
float
- class aabbtree.AABBTree(aabb=AABB(None), value=None, left=None, right=None)[source]
Bases:
objectStatic AABB Tree
An AABB tree where the bounds of each AABB do not change.
- Parameters:
aabb (AABB) – An AABB
value – The value associated with the AABB
left (AABBTree, optional) – The left branch of the tree
right (AABBTree, optional) – The right branch of the tree
- add(aabb, value=None, method='volume')[source]
Add node to tree
This function inserts a node into the AABB tree. The function chooses one of three options for adding the node to the tree:
Add it to the left side
Add it to the right side
Become a leaf node
The cost of each option is calculated based on the method keyword, and the option with the lowest cost is chosen.
- Parameters:
aabb (AABB) – The AABB to add.
value – The value associated with the AABB. Defaults to None.
method (str) –
The method for deciding how to build the tree. Should be one of the following:
volume
volume Costs based on total bounding volume and overlap volume
Let \(p\) denote the parent, \(l\) denote the left child, \(r\) denote the right child, \(x\) denote the AABB to add, and \(V\) be the volume of an AABB. The three options to add \(x\) to the left branch, add it to the right branch, or create a new parent. The cost associated with each of these options is:
\[\begin{split}C(\text{add left}) &= V(p \cup x) - V(p) + V(l \cup x) - V(l) + V((l \cup x) \cap r) \\ C(\text{add right}) &= V(p \cup x) - V(p) + V(r \cup x) - V(r) + V((r \cup x) \cap l) \\ C(\text{create parent}) &= V(p \cup x) + V(p \cap x)\end{split}\]In the add-left cost, the term \(V(b \cup x) - V(b)\) is the increase in parent bounding volume. The cost \(V(l \cup x) - V(l)\) is the increase in left child bounding volume. The last term, \(V((l \cup x) \cap r)\) is the overlapping volume between children if \(x\) were added to the left child. The cost to create a new parent is the bounding volume of the parent and \(x\) plus their overlap volume.
This cost function includes the increases in bounding volumes and the amount of overlap- two values a balanced AABB tree should minimize. The cost function suits the author’s current needs, though other applications may seek different tree properties. Please visit the AABBTree repository if interested in implementing another cost function.
- does_overlap(aabb, method='DFS', closed=False)[source]
Check for overlap
This function checks if the limits overlap any leaf nodes in the tree. It returns true if there is an overlap.
New in version 2.6.0
This method also supports overlap checks with another instance of the AABBTree class.
- Parameters:
aabb (AABB or AABBTree) – The AABB or AABBTree to check.
method (str) – {‘DFS’|’BFS’} Method for traversing the tree. Setting ‘DFS’ performs a depth-first search and ‘BFS’ performs a breadth-first search. Defaults to ‘DFS’.
closed (bool) – Option to specify closed or open box intersection. If open, there must be a non-zero amount of overlap. If closed, boxes can be touching.
- Returns:
True if overlaps with a leaf node of tree.
- Return type:
bool
- overlap_aabbs(aabb, method='DFS', closed=False, unique=True)[source]
Get overlapping AABBs
This function gets each overlapping AABB.
New in version 2.6.0
This method also supports overlap checks with another instance of the AABBTree class.
- Parameters:
aabb (AABB or AABBTree) – The AABB or AABBTree to check.
method (str) – {‘DFS’|’BFS’} Method for traversing the tree. Setting ‘DFS’ performs a depth-first search and ‘BFS’ performs a breadth-first search. Defaults to ‘DFS’.
closed (bool) – Option to specify closed or open box intersection. If open, there must be a non-zero amount of overlap. If closed, boxes can be touching.
unique (bool): Return only unique pairs. Defaults to True.
- Returns:
AABB objects in AABBTree that overlap with the input.
- Return type:
list
- overlap_values(aabb, method='DFS', closed=False, unique=True)[source]
Get values of overlapping AABBs
This function gets the value field of each overlapping AABB.
New in version 2.6.0
This method also supports overlap checks with another instance of the AABBTree class.
- Parameters:
aabb (AABB or AABBTree) – The AABB or AABBTree to check.
method (str) – {‘DFS’|’BFS’} Method for traversing the tree. Setting ‘DFS’ performs a depth-first search and ‘BFS’ performs a breadth-first search. Defaults to ‘DFS’.
closed (bool) – Option to specify closed or open box intersection. If open, there must be a non-zero amount of overlap. If closed, boxes can be touching.
unique (bool): Return only unique pairs. Defaults to True.
- Returns:
Value fields of each node that overlaps.
- Return type:
list
- property depth
Depth of the tree
- Type:
int
- property is_leaf
returns True if is leaf node
- Type:
bool
Contributing
Contributions to the project are welcome. Please visit the AABBTree repository to clone the source files, create a pull request, and submit issues.
Publication
If you use AABBTree in you work, please consider including this citation in your bibliography:
K. A. Hart and J. J. Rimoli, Generation of statistically representative microstructures with direct grain geomety control, Computer Methods in Applied Mechanics and Engineering, 370 (2020), 113242. (BibTeX) (DOI)
The incremental insertion method is discussed in section 2.2.2 of the paper.
License and Copyright Notice
Copyright © 2019-2023, Georgia Tech Research Corporation
AABBTree is open source and freely available under the terms of the MIT license.
License
MIT License
Copyright (c) 2019-2024 Georgia Tech Research Corporation
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.


